Transpose Matriks: Pengertian, Sifat, Contoh Soal dan Pembahasannya

JAKARTA, iNews.id - Transpose matriks merupakan salah satu materi dalam pelajaran matematika. Tahukah kamu bagaimana mengoperasikan transpose matriks? Yuk simak ulasan berikut.

Pengertian Transpose Matriks

Transpose matriks adalah matriks ubahan dari matriks lain yang sudah ada sebelumnya dan unsur-unsur barisnya menjadi unsur-unsur kolom dan unsur-unsur kolomnya menjadi unsur baris. Dalam matriks ini perlu diingat bahwa baris pertama harus menjadi kolom pertama atau sebaliknya kolom pertama menjadi baris pertama.

Sebagai contoh, transpose matriks dari matriks A adalah suatu matriks yang diperoleh dari matriks A, dengan cara memindahkan elemen-elemen baris menjadi elemen pada kolom dan memindahkan elemen-elemen kolom menjadi elemen pada baris. Transpose dari matriks A dinyatakan dengan: AT atau At

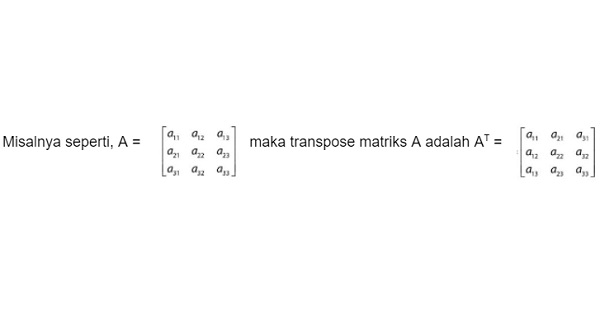
Sifat-sifat Transpose Matriks

Adapun sifat-sifat dari transpose matriks yang membedakan dari jenis matriks lainnya, yaitu di antaranya sebagai berikut.

(AT)T = A
(kA)T = k (A)T , k merupakan konstanta
(AB)T = BTAT
(A+B)T = AT + BT

Transpose Matriks dan Contohnya

Adapun contoh soal transpose matriks beserta pembahasannya yang dikutip dari berbagai macam sumber, yaitu sebagai berikut.

4. Carilah transpose matriks di bawah ini

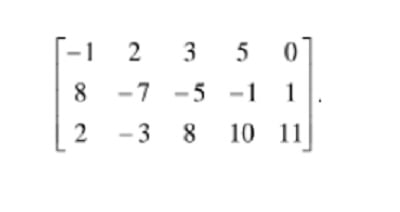
Pembahasan:

Pencarian transpose matriks dengan menggunakan transpose (B)
Maka, B = [-1 2 3 5 0; 8 -7 -5 -1 1; 2 -3 8 10 11]

B =
-1 2 3 5 0
8 -7 -5 -1 1
2 -3 8 10 11

Transpose (B), menjadi sebagai berikut.

-1 8 2
2 -7 -3
3 -5 8
5 -1 10
0 1 11

Maka diperoleh:

a = 2

-a + b - 3 = -1

-2 + b = 2

b = 4

Sehingga, a + b = 2 + 4 = 6

Itulah transpose matriks dengan contoh soal dan pembahasannya yang dapat kamu pelajari. Semoga artikel ini menambah pemahaman kamu mengenai transpose matriks ya, selamat belajar!