Cara Menghitung KPK dan FPB Mudah, Lengkap Contoh dan Jawabannya

JAKARTA, iNews.id - KPK dan FPB adalah materi matematika yang sering dipelajari di sekolah. Setiap siswa harus mengerti bagaimana cara menentukan KPK dan FPB agar bisa menjawab soal yang diberikan. Simak di sini informasinya.

Pengertian FPB dan KPK dan Contohnya

KPK: Kelipatan Persekutuan Terkecil

Melansir buku Sukses Ujian Nasional SD 2020 karya Esvandiari, suatu bilangan merupakan kelipatan dari bilangan lain jika bilangan lain tersebut merupakan hasil perkalian dengan bilangan yang dimaksud.

Kelipatan suatu bilangan didapatkan dari mengalikannya dengan bilangan asli. Kelipatan persekutuan adalah himpunan semua kelipatan yang sama dari dua bilangan atau lebih. KPK adalah bilangan paling kecil dari himpunan kelipatan persekutuan dua bilangan atau lebih.

Cara menentukan KPK

Contoh KPK dari 4, 6, dan 8:
Kelipatan (4) = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, }
Kelipatan (6) = (6, 12, 18, 24, 30, 36, 42, 48, }
Kelipatan (8) = {8, 16, 24, 32, 40, 48, }
Kelipatan persekutuan 4, 6, dan 8 = 24, 48, }
Jadi KPK 4, 6, dan 8 adalah 24.

Faktorisasi prima adalah pemecahan suatu bilangan menjadi bentuk perkalian dengan faktor-faktor prima. Pencarian faktorisasi prima dapat dilakukan dengan pohon faktor.
Contoh KPK dari 4, 6, dan 8:

Faktorisasi prima dari 4 = 2
Faktorisasi prima dari 6 = 2 x 3
Faktorisasi prima dari 8 = 2

Langkah selanjutnya, ambil semua faktor. Jika ada faktor yang sama, ambil yang pangkatnya besar.

Jadi, KPK dari 4, 6, dan 8 = 2 x 3 = 24

Contoh soal: KPK dari 10, 15, dan 25 adalah

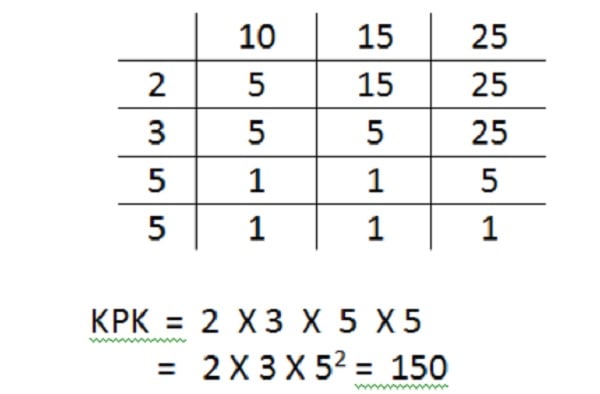
Dalam mencari KPK menggunakan tabel, maka bagi bilangan dengan yang terkecil dan posisikan angka pembagi sebelah kiri pada tabel. Jadi, KPK dari 10, 15, dan 25 adalah 150.

FPB: Faktor Persekutuan Terbesar

Faktor adalah pembagi atau hasil bagi suatu bilangan asli yang menghasilkan sisa nol. Bilangan yang bisa membagi bilangan lain dengan tidak bersisa merupakan faktor bilangan tersebut. Faktor persekutuan adalah himpunan dari semua faktor-faktor yang sekutu (sama) dari dua bilangan atau lebih. FPB adalah suatu bilangan yang diperoleh dari faktor persekutuan dua bilangan atau lebih yang paling besar.

Cara menentukan FPB

Contoh FPB dari 6, 9, dan 12:
Faktor (6) = {1, 2, 3, 6}
Faktor (9) = {1, 3, 9}
Faktor (12) = {1, 2, 3, 4, 6, 12}
Maka FPB dari 6, 12, dan 16 adalah 3.

Caranya dengan mengalikan antar faktor prima sekutu yang mempunyai pangkat paling kecil.
Contoh FPB dari 16 dan 20
Faktorisasi prima dari 16 = 2 x 2
Faktorisasi prima dari 20 = 2 x 5
Maka FPB dari 16 dan 20 = 2 = 4

Contoh soal: FPB 75, 105, dan 120 adalah

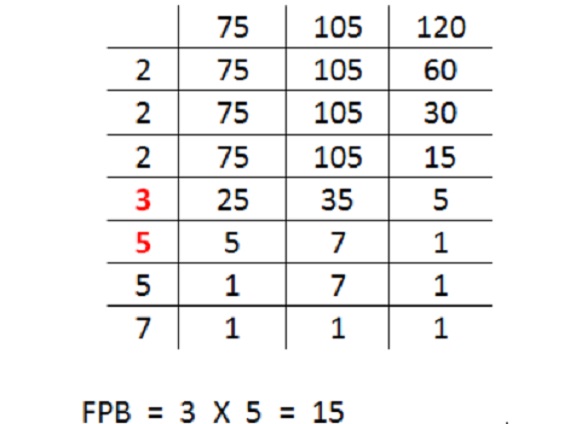
Jadi dapat diperoleh FPB dari 75, 105, dan 60 adalah 15.

Sebelum masuk ke soal cerita KPK dan FPB, sebaiknya kita mengetahui kata kunci berikut ini agar bisa membedakan antara soal cerita KPK dan FPB.

KPK:
Setiap sekali,
Bersama-sama
Bersamaan,
Bersama lagi

FPB:
Paling banyak, sama banyak,
Sebanyak-banyaknya,
Jumlah yang sama,
Jenis yang sama,
Sama rata

Dion mengunjungi perpustakaan setiap 6 hari sekali, Beni setiap 4 hari sekali, sedangkan Sukma setiap 8 hari sekali. Jika pada tanggal 28 Januari mereka mengunjungi perpustakaan bersama-sama, pada tanggal berapa mereka akan mengunjungi perpustakaan bersama-sama lagi berikutnya?

Jawab:
Faktorisasi prima dari 4 = 2
Faktorisasi prima dari 6 = 2 x 3
Faktorisasi prima dari 8 = 2
KPK dari 4, 6, dan 8 = 2 x 3 = 24
Jadi, mereka mengunjungi perpustakaan bersama lagi setelah 24 hari.

Tersedia 84 buku, 56 pensil, dan 140 krayon. Jika buku, pensil, dan krayon tersebut akan dibagi rata kepada sejumlah anak, berapa anak sebanyak-banyaknya yang dapat menerima pembagian tersebut?

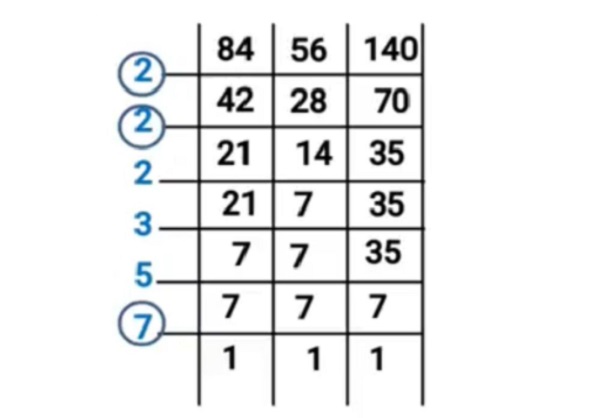
FPB 2 x 2 x 7 = 28
Jadi, banyak anak yang dapat menerima pembagian tersebut adalah 28 anak.

Nah itu dia bagaimana cara cepat menentukan KPK dan FPB.Semoga kamu segera dapat memahami materi KPK dan FPB dengan mudah ya. Selamat belajar!